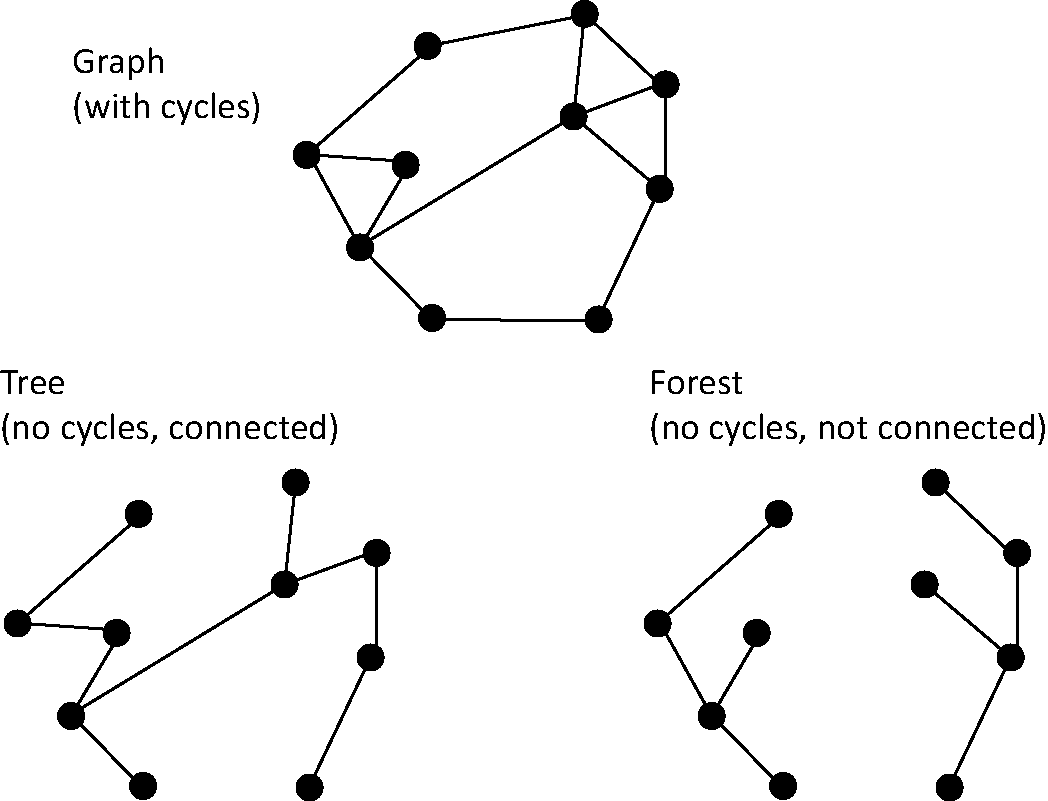
Tree

A tree is a connected graph that has no cycles.

A "forest" is a graph with no cycles, but are not connected, composed of "Leaves".
A forest connected with an Articulation Point will turn it into a tree, otherwise, it is a disconnected Graph.

Graph vs Trees vs Forests.png

Theorem

Let $T$ be a graph with n vertices. Then the following statements are equivalent:

$T$ is a tree;
$T$ contains no cycles, and has $n — 1$ edges;
$T$ is connected, and has $n - 1$ edges;
$T$ is connected, and each edge is a bridge;
any two vertices of $T$ are connected by exactly one path;
$T$ contains no cycles, but the addition of any new edge creates exactly one cycle.

A subgraph that contains all vertices of the original graph

G

that is a tree (no cycles).

a Labeled Tree is a tree wherein the order and degree of each point matters.
We can find the number of Labeled Trees of an $n$ -vertex tree with Cayley's Formula.

Spanning Tree Example.png