Created: 2023-12-11 05:23
Status: #concept
Subject: Programming
Tags: Graph Multidimensional Array Adjacency List
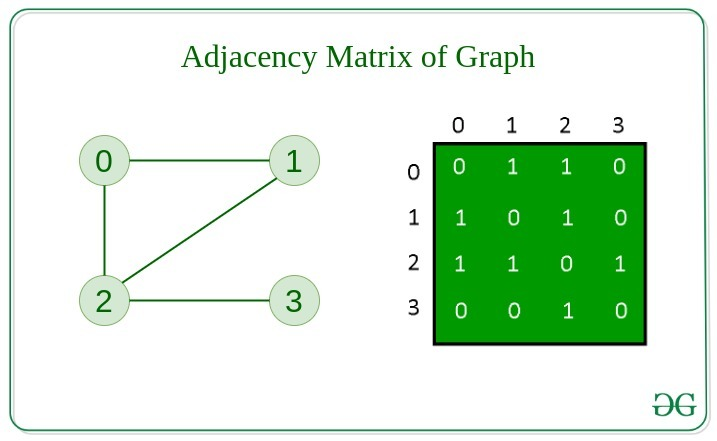
Adjacency Matrix
We can store the graph in a 2D matrix containing boolean values
1 or 0 where the edge (1,2) can be represented as matrix[1][2].
- the
rowis thesource. - the
colis thedestination.
Implementation
MAX is the number of possible vertices, so the space complexity of a graph is O(N * N), where N is MAX vertices.
G[src][dest]can be1denoting a connection, or it can equal to theweightof a graph for Weighted Graphs.
typedef int Graph[MAX][MAX];
void init(Graph G) {
for (int row = 0; row < MAX; row++) {
for (int col = 0; col < MAX; col++) {
G[row][col] = 0;
}
}
}
Operations
void addEdge(Graph G, int src, int dest) { G[src][dest] = 1; }
bool edgeExists(Graph G, int src, int dest) {
return G[src][dest] == 1 ? true : false;
}
Breadth-First Search
- We enqueue the
rootnode to scan in ournodesToVisitqueue and mark it asvisited[root] = 1; - While
nodesToVisitis not empty: - We visit all nodes
xof the front Node innodesToVisitand if they arevisited[x] == 0, mark them asvisited[x] = 1andenq(Q, x)them. - We
deq(Q)and print the element dequeued.
Time complexity is
O(V+E).
void bfs(Graph G, int root) {
// if node is visited, visited[node] == 1
Set visited = {0};
// a queue of the current nodes to process, before inserting to Set
Queue Q = initQueue();
if (Q != NULL) {
// mark the root as visited & enqueue it
visited[root] = 1;
enq(Q, root);
while (!isEmpty(Q)) {
int x;
for (x = 0; x < MAX; x++) {
// if the current queue node is adjacent to node x & we didn't visit x
if (G[Q->front->data][x] == 1 && !visited[x]) {
visited[x] = 1; // mark x as visited
enq(Q, x); // enqueue x to visit all its nodes later
}
}
// print the element we enqueued
printf("%d ", deq(Q));
}
}
puts("");
}